Willkommen
Lehre
- Programmierung a & b, Angewandte Mathematik Bachelor
lms.bht-berlin.de/course/view.php - Epidemics on Networks, Mathematik Bachelor
lms.bht-berlin.de/course/view.php
| Semester | Veranstaltungsname | Studiengang | Fachsemester |
|---|---|---|---|
| Winter 2020/2021 | Grundlagen des mathematischen Arbeitens | Angewandte Mathematik Bachelor | 1 |
| Mathematik I | Technische Informatik Bachelor | 1 | |
| Mathematik II | Medieninformatik Bachelor | 2 | |
| Sommer 2020 | Datenstrukturen und Algorithmen | Mathematik Bachelor | 4 |
| Mathematik I | Medieninformatik Bachelor | 1 | |
| Mathematik II | Technische Informatik Bachelor | 2 | |
| Winter 2019/2020 | Grundlagen des mathematischen Arbeitens | Angewandte Mathematik Bachelor | 1 |
| Mathematik I | Technische Informatik Bachelor | 1 | |
| Mathematik II | Medieninformatik Bachelor | 2 | |
| Sommer 2019 | Programmierung II a+b | Mathematik Bachelor | 2 |
| Mathematik I | Medieninformatik Bachelor | 1 | |
| Winter 2018/2019 | Programmierung I a+b | Mathematik Bachelor | 1 |
| Mathematik II | Technische Informatik Bachelor | 2 | |
| Sommer 2018 | Mathematik I | Technische Informatik Bachelor | 1 |
| Mathematik II | Medieninformatik Bachelor | 2 | |
| Lineare Algebra | Medieninformatik-Online Bachelor | 1 | |
| Winter 2017/2018 | Anwendungsprogrammierung | Mathematik Bachelor | 5 |
| Mathematik I | Medieninformatik Bachelor | 1 | |
| Lineare Algebra | Medieninformatik-Online Bachelor | 1 | |
| Winter 2016/2017 | Anwendungsprogrammierung | Mathematik Bachelor | 5 |
| Mathematik II | Medieninformatik Bachelor | 2 | |
| Lineare Algebra | Medieninformatik-Online Bachelor | 1 | |
| Sommer 2016 | Mathematik I | Medieninformatik Bachelor | 1 |
| Mathematik II | Medieninformatik Bachelor | 2 | |
| Winter 2015/2016 | Anwendungsprogrammierung | Mathematik Bachelor | 5 |
| Mathematik II | Medieninformatik Bachelor | 2 | |
| Mathematik II | Technische Informatik Bachelor | 2 | |
| Sommer 2015 | Anwendungsprogrammierung | Mathematik Bachelor | 5 |
| Mathematik I | Medieninformatik Bachelor | 1 | |
| Mathematik I | Technische Informatik Bachelor | 1 | |
| Winter 2014/2015 | Datenstrukturen und Algorithmen | Mathematik Bachelor | 4 |
| Mathematik II | Medieninformatik Bachelor | 2 | |
| Mathematik II | Technische Informatik Bachelor | 2 | |
| Sommer 2014 | Datenstrukturen und Algorithmen | Mathematik Bachelor | 4 |
| Mathematik I | Medieninformatik Bachelor | 1 | |
| Mathematik I | Technische Informatik Bachelor | 1 | |
| Lineare Algebra | Medieninformatik-Online Bachelor | 1 | |
| Winter 2013/2014 | Diskrete Mathematik | Mathematik Bachelor | 3 |
| Programmieren II | Mathematik Bachelor | 2 | |
| Sommer 2013 | Operations Research | Mathematik Bachelor | 5 |
| Programmieren I | Mathematik Bachelor | 1 | |
| Brückenkurs Mathematik | Mathematik BAchelor | 1 | |
| Winter 2012/2013 | Lineare Algebra | Medieniformatik-Online Bachelor | 1 |
| Programmieren II | Mathematik Bachelor | 1 | |
| Sommer 2012 | Lineare Algebra | Medieninformatik-Online Bachelor | 1 |
| Programmieren I+II | Mathematik Bachelor | 1 | |
| Diskrete Mathematik | Mathematik Bachelor | 3 | |
| Winter 2010/2011 | Programmieren II+IV | Mathematik Bachelor | 2 |
| Lineare Algebra | Medieninformatik-Online Bachelor | 1 | |
| Brückenkurs | Mathemaik Bachelor | 1 | |
| Sommer 2010 | Programmieren I+II | Mathematik Bachelor | 1 |
| Lineare Algebra | Medieninformatik-Online Bachelor | 1 | |
| Winter 2009/2010 | Mathematik II | Medieninformatik Bachelor | 2 |
| Lineare Algebra | Medieninformatik-Online Bachelor | 1 | |
| Anwendungsprogrammierung | Mathematik Bachelor | 5 | |
| Sommer 2009 | Mathematik I | Medieninformatik Bachelor | 1 |
| Lineare Algebra | Medieninformatik-Online Bachelor | 1 | |
| Grundlagen der Mathematik | Wirtschaftsinformatik-Online Bachelor | 1 |
- „Modellieren von Ansteckungsdiffusionen in mehrschichtigen Netzwerken", Januar 2021
- „Optimale Beladung von Containern unter Berücksichtigung der Gleichgewichtsverteilung", Dezember 2018
- „Ein Framework zur Generierung eines synthetischen Multiplex-Netzwerks zur Emulation von Personenverkehrsnetzwerken", Januar 2017
- „Evaluierung ausgewählter Algorithmen zur Erkennung von Stauschwerpunkten im urbanen Straßennetz“, September 2016
- „Näherungsansätze für das geschachtelte Rucksackproblem“, Februar 2016.
- „Ein mathematisches Modell zur dynamischen Ressourcenplanung an einem Praxisbeispiel“, Juli 2014
- „Ein Algorithmus zur Lösung eines volkswirtschaftlichen Entscheidungsproblems“, Februar 2012
- „Optimale Zuordnung- Implementierung eines Matching-Algorithmus für vollständig bipartite Graphen“, März 2010
- „A GRASP-Heuristic for the Minimum Graph Bisection Problem“, TU Darmstadt, März 2007
- „A Greedy Randomized Adaprive Search Procedure for the Minimum Graph Bisection Problem“, TU Darmstadt, Juni 2006.
- „Selected General Purpose Heuristics for Solving Mixed Integer Programs“, Diplomarbeit, TU Darmstadt,, März 2006
- „A Heuristic for Finding Cycle Inequalities for the Node Capacitated Graph Partitioning Problem“, Bachelorarbeit, TU Darmstadt, Februar 2005.
- Die Bachelorarbeiten, die ich aktuell betreue, beschäftigen sich rund um die Multiplex-Netzwerke, die unter "Aktuelle Forschungsprojekte" erläutert sind. Hier ein paar Themenbeispiele:
- Generierung von synthetischen Multiplex-Netzwerken
- Statistische Validierung randomisierter Verfahren zur Generierung von synthetischen Multiplex-Netzwerken
- Untersuchung der Verletztlichkeit der Multiplex-Netzwerke, existierende reelle Multiplexe und ihre synthetischen Nachbildungen im Vergleich
- Ansteckungsdiffusionen in Multiplex-Netzwerken
- Themen im Bereich Diskreter Optimierung oder Operations Reseach, die in der Praxisphase vorkommen, sind willkommen. Ein Programmieranteil wird vorausgesetzt (C/C++, Java/JavaFX, Python).
Forschung
- Lineare gemischt-ganzzahlige Optimierung, kombinatorische Optimierung, semidefinite Optimierung
- Operations Research
- Algorithmische Graphentheorie
- Netzwerktheorie - Multiplex-Netzwerke
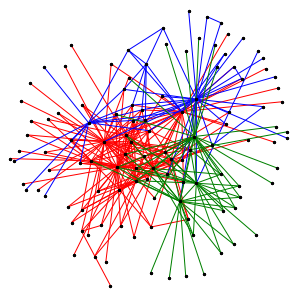
Generative Methoden zur Emulation Multiplex-Netzwerke
Die Untersuchung der Fülle von in der Praxis vorkommenden Netzwerke hat ergeben, dass sie sich durch die Überlagerung von mehreren kleineren Subnetzen charakterisieren lassen. Als Beispiele seien Infrastruktur der Fluglinien, Korrelationen von Finanzanlagen, ökologische Systeme, und nicht zuletzt die Vielfalt der Kommunikationswege in sozialen Netzwerken. Die Subnetze sind Gruppen von Knoten, die stärker miteinander als mit dem Rest des Netzwerks verbunden sind, und werden in Abhängigkeit von des Netzwerkstyps als Communities (Gemeinschaften) oder Layers (Schichten) bezeichnet. Diese komplexen Netzwerke nennt man Multiplex-Netzwerke. Eine Community, eine Schicht entsteht durch eine Art von Relation, die die Gruppe von Knoten verbindet. Beispielsweise werden Einzelpersonen (Knoten) in einem sozialen Netzwerk verlinkt (mit einer Kante verbunden), wenn sie gemeinsam kommunizieren. Die Kommunikation kann per SMS, Email oder Telefonanruf erfolgen. Jeder Kommunikationstyp erzeugt eine Relationsschicht, eine Community. Ein weiteres Multiplex-Netzwerk entsteht beispielsweise, wenn Einzelpersonen über ihre gemeinsamen Interessen verlinkt werden: Gleiche Interessen bilden hier eine Community.
Die aktuellen Fragestellungen der Netzwerktheorie beziehen sich nicht nur auf die Topologie - die räumliche Struktur - des globalen Multiplex-Netzwerks, sondern auch auf seinen Entstehungsprozess und insbesondere die Bildung der dazugehörigen Communities. In manchen Multiplex-Netzwerken formen sich die Communities über die Zeit unabhängig von anderen, in manch anderen basiert das Entstehen einer neuen Community auf den schon existierenden.
Die Generierung synthetischer Netzwerke ist ein lebendiger Bereich der Netzwerkwissenschaften. Mehrere Modelle für einschichtige synthetische Netzwerke wurden in der letzten Dekade präsentiert. Weniger verbreitet sind Modelle auf der Basis eines Multiplexes. Die aktuell bekannten Modelle verwenden die Methode des so genannten Preferential Attachments, die Netzwerke mit skalenfreien Struktur nachbildet.

- M. Fügenschuh, R. Gera, A. Tagarelli
„ Structural and Spectral Properties of Synthetic Models for Multilayer Networks", in Vorbereitung, 2021 - M. Fügenschuh, R. Gera, A. Tagarelli
„Topological Analysis of Synthetic Models for Air Transportation Multilayer Networks", 2021 - M. Fügenschuh, R. Gera, A. Tagarelli
„ANGEL: A Synthetic Model for Airline Network Generation Emphasizing Layers", 2020 - M. Fügenschuh, R. Gera, T. Lory
„A Synthetic Model for a Multilevel Network", 2017. - M. Fügenschuh, R. Gera, M. Heaton
„Synthetic Models for Multi-Layered Networks", erweiterter Abstrakt, 2017 - M. Ludszuweit, A. Mojsic, J. Sokół, A. Fügenschuh, M. Fügenschuh
„Mathematical Optimization of a Magnetic Ruler Layout With Rotated Pole Boundaries“, 2015 - M. Ludszuweit, A. Mojsic, J. Sokół, A. Fügenschuh, M. Fügenschuh
„Mathematical Model for Absolute Magnetic Measuring Systems in Industrial Applications“, 2015 - A. Armbruster, C. Helmberg, M. Fügenschuh, A. Martin
„LP and SDP Branch-and-Cut Algorithms for the Minimum Graph Bisection Problem: A Computational Comparison“, 2012 - M. Fügenschuh
„Structure Dependent Inequalities for the Bisection Cut Polytope“, 2010 - M. Armbruster, M. Fügenschuh, C. Helmberg, A. Martin
„On the Graph Bisection Polytope“, 2008 - M. Armbruster, M. Fügenschuh, C. Helmberg, A. Martin
„A Comparative Study of Linear and Semidefinite Branch-and-Cut Methods for Solving the Minimum Graph Bisection Problem“, 2008 - A. Fügenschuh, M. Fügenschuh
„Integer Linear Programming Models for Topology Optimization in Sheet Metal Design“, 2008 - M. Fügenschuh
„Relaxations and Solutions for the Minimum Graph Bisection Problem“,
Doktorarbeit, 2007 - M. Armbruster, M. Fügenschuh, C. Helmberg, N. Jetchev, A. Martin
„Hybrid Genetic Algorithm within Branch-and-Cut for the Minimum Graph Bisection Problem“, 2006 - M. Armbruster, M. Fügenschuh, C. Helmberg, N. Jetchev, A. Martin
„LP-based Genetic Algorithm for the Minimum Graph Bisection Problem“, 2005
December 2020 „Topological Analysis of Synthetic Models for Air Transportation Multilayer Networks “ (Poster)
Complex Networks 2020: The 9th International Conference on Complex Networks and Their Applications.
Juni 2019 „ANGEL - Air Networks Generation Emphasizing Layers“
30th European Conference on Operational Research, Dublin.
Dezember 2017 „Synthetic Models for Multi-Layered Networks“ (Poster)
Complex Networks 2017: The 6th International Conference on Complex Networks and Their Applications, Lyon, Frankreich.
September 2017 „Synthetic Models Multilevel Networks“
International Conference on Operations Research OR2017, Berlin.
Februar 2017 „A Generative Model for a Random Multiplex Network“
Seminar on Network Sciences, Naval Postgraduate School Monterey, CA, USA.
September 2015 „Mathematical Optimization of a Magnetic Ruler Layout With Rotated Pole Boundaries“
International Conference on Opertions Research OR2015, Wien.
März 2015 „Anwendungsorientierte Lehre und Forschung an einer Hochschule“
Workshop Women in Optimization, Heidelberg.
August 2012 „LP and SDP branch-and-cut algorithms for the minimum graph bisection problem: A computational comparison“
21st International Symposium on Mathematical Programming, Berlin.
Februar 2012 „Branch-and-Cut Methods for Solving the Graph Bisection Problem“
Discrete Optimization Seminar at H. Milton Stewart School of Industrial and Systems Engineering at Georgia Technology Institute, Atlanta/USA
September 2007 „A Comparative Study of Linear and Semidefinite Branch-and-Cut Methods for Solving the Minimum Graph Bisection Problem“
1st Warsaw Seminar on Industrial Mathematics, Warschau, 18. - 19. März 2010.
März 2010 „Solving the Minimum Graph Bisection Problem with Linear and Semidefinite Relaxations“
13th Czech-French-German Conference on Optimization, Heidelberg.
Oktober 2006 „Lineare und Semidefinite Relaxierungen für das Minimum Graph Bisektion Problem“
Seminar für Kombinatorik und Graphentheorie, Technische Universität Warschau.
August 2006 „Polyhedral and Semidefinite Relaxations for Graph Bisection Problems“
19. International Symposium on Mathematical Programming, Rio de Janeiro.
August 2006 „Polyhedral Relaxations for Graph Bisection Problems“,
Seminar für Optimierung, Fachbereich Mathematik, Universität São Paulo.
Juli 2006 „Warum spart der Staat Steuern, wenn Schüler eine halbe Stunde früher aufstehen? - Theorie und Praxis der Diskreten Optimierung“
Schnuppertage für Schülerinnen an der TU Darmstadt, Fachbereich Mathematik.
April 2006 „Hybrid Genetic Algorithm within Branch-and-Cut for the Minimum Graph Bisection Problem“,
6th European Conference on Evolutionary Computation in Combinatorial Optimization EvoCOP06, Budapest.
September 2005 „Strong Valid Inequalities for the Graph Bisection Polytope“
Conference on Operations Research OR2005, Bremen.
August 2005 „The Ellipsoid Method for Linear Programming“
Workshop on Optimization and Scientific Computing, Hirschegg.
Juni 2005 „Discrete Optimization Methods in Portfolio Selection“
MathFinance Colloquium, Hochschule fü̈r Bankwirtschaft Frankfurt.
