Mathematik und Informatik
seit dem 1.10.2011 im Ruhestand
Der Mensch soll arbeiten, aber nicht wie ein Lasttier, das unter seiner Bürde in den Schlaf sinkt und nach der notdürftigsten Erholung der erschöpfenden Kraft zum Tragen derselben Bürde wieder aufgestört wird. Er soll angstlos, mit Lust und Freudigkeit arbeiten und Zeit übrigbehalten, seinen Geist und sein Auge zum Himmel zu erheben, zu dessen Anblick er gebildet ist.
Johann Gottlieb Fichte (1762-1814)

Neben der Arbeit braucht der Mensch einen Ausgleich. Hier einige Links aus dem Sport-Bereich, die mir viel bedeuten:
VfL Zehlendorf e. V. Berlin-Marathon Berlin-Marathon Jubilee Club Kienbaum
Nobelpreise ...
Pardon, ich langweile Sie. Natürlich sind Ihnen die Gebiete der Nobelpreise geläufig (Medizin, Physik, Chemie, Literatur, Friedensbemühungen). Vielleicht wissen Sie sogar, dass es den Nobelpreis für Wirtschaftswissenschaften im strengen Sinne nicht gibt, dass es vielmehr ein Preis der schwedischen Reichsbank zum Gedenken an Alfred Nobel ist, der aber allgemein auch als Nobelpreis bezeichnet wird. Und natürlich erfahren Sie jährlich in allen Nachrichtensendungen (Radio, Tagesschau, Heute), wer welchen dieser Preise im laufenden Jahr erhalten wird. Da Sie als gebildeter Mensch so ausgezeichnet informiert sind, endet dieser Abschnitt hier ...
Der Niels Henrik Abel Gedächtnisfond (Niels Henrik Abels minnefond) wurde im Jahr 2002 zur 200. Wiederkehr des Geburtstages dieses bedeutenden Mathematikers von der Norwegischen Regierung ins Leben gerufen. Der Abelpreis für Mathematik wird seit 2003 jährlich vergeben. Dieser Preis ist nach Dotierung (derzeit rund 750.000 €) und Bedeutung den Nobelpreisen vergleichbar.
Der Abelpreis für Mathematik wurde bisher (Herbst 2017) 15 Mal vergeben, er wird im Jahr 2018 also zum 16. Mal vergeben werden. Haben Sie jemals von diesem Preis in einer Zeitung gelesen? (Sie lesen doch eine Zeitung von Niveau und nicht die Bild-Zeitung, oder?). Erinnern Sie sich, diese Nachricht irgendwo in Tagesschau oder Heute gehört zu haben? Nein? Na, dann haben Sie sicherlich nicht aufgepasst, oder?
Wenn man in Diskussionen darauf hinweist, dass der Mathematik-Unterricht früher in deutschen Schulen ein höheres Niveau besessen habe, wird man häufig mit der Bemerkung abgespeist, dass dies nur die übliche Klage älterer Leute sei nach dem Motto "früher war alles besser ...".
Da hilft nur ein Vergleich der Lehrpläne, der verwendeten Aufgaben.
Beim Aufräumen fiel mir eine alte Ausgabe der Schulzeitschrift meiner Schule, der Albrecht-Thaer-Schule vor dem Holstentor (Hamburg), in die Hände (es gibt diese Schule leider nicht mehr, es gibt nur eine Albrecht-Thaer-Schule in Hamburg-Stellingen). Es ist die Ausgabe mit der lfd. Nummer 45, erschienen im 44. Jahrgang. Dort findet man die folgenden Abituraufgaben Mathematik für die Klasse 13n (mathematisch-naturwissenschaftlicher Zweig; Reifeprüfung 1970):
1. Aufgabe:
Gegeben ist eine gerader Zylinder (Grundkreisradius r und Höhe h). Durch konzentrische Bohrung soll aus diesem Zylinder ein weiterer Zylinder herausgebohrt werden, und zwar derart, dass die gesamte Oberfläche des verbleibenden Restkörpers (innerer und äußerer Mantel sowie oberer und unterer Kreisring) einen möglichst großen Inhalt hat. Ist dieses Problem bei beliebiger Wahl von r und h stets lösbar? Wie lauten im Falle der Lösbarkeit die Maße für den Bohrungsradius und den maximalen Oberflächeninhalt?
2. Aufgabe:
Gegeben sind die beiden Funktionen

Welche Gruppe bezüglich Verkettung wird von diesen Funktionen erzeugt? Beweisen Sie die Gruppeneigenschaft!
Erläutern Sie den Begriff des Gruppentyps und geben Sie an, von welchem Ihnen bekannten Gruppentyp diese Gruppe ist (Beweis).
Skizzieren Sie die Graphen der zur Gruppe gehörigen Funktionen bezüglich des gleichen Koordinatensystems und erläutern Sie auch daran das Erfülltsein der Gruppenpostulate (N) und (I).
3. Aufgabe:
Geben Sie eine graphische Darstellung der Punktmenge
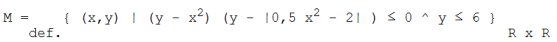
und begründen Sie Ihr Ergebnis! Besitzt M eine Symmetrieeigenschaft?
Berechnen Sie den Flächeninhalt von M, und vergleichen Sie das mit Rechenstabgenauigkeit angegebene Ergebnis mit dem durch Abschätzung aus der Zeichnung gewonnenen!
Verstehen Sie, dass ich meinen Lehrern noch heute dankbar bin für die gute Ausbildung, die uns in der Schule zuteil wurde?
1. Beweis:
Dieser Beweis wendet sich an Schüler der 7. Klasse. Er verwendet nur die 4 Grundrechenarten und Regeln zur Umformung von Gleichungen.

2. Beweis:
Dieser Beweis wendet sich an Schüler der 8. oder 9. Klasse.

3. Beweis:
Dieser Beweis wendet sich an Schüler ab der 11. Klasse, die eine Einführung der komplexen Zahlen im Unterricht hatten (in der Regel geschieht dies im Leistungskurs Mathematik der 11. Klasse). Er wendet sich auch an Ingenieurstudenten z. B. der Elektrotechnik, die komplexe Zahlen in ihren Berechnungen nutzen.




